Logistic regression is borrowed from statistics. You can use this for classification problems. Given an image, is it class 0 or class 1?

The word “logistic regression” is named after its function “the logistic”. You may know this function as the sigmoid function.

Related Course:
Deep Learning with TensorFlow 2 and Keras

Introduction

Sigmund function

Logisitic regression uses the sigmund function for classification problems. What is this function exactly?

The sigmund function is:

1 / (1 + e^-t)

It’s an s-shaped curve.

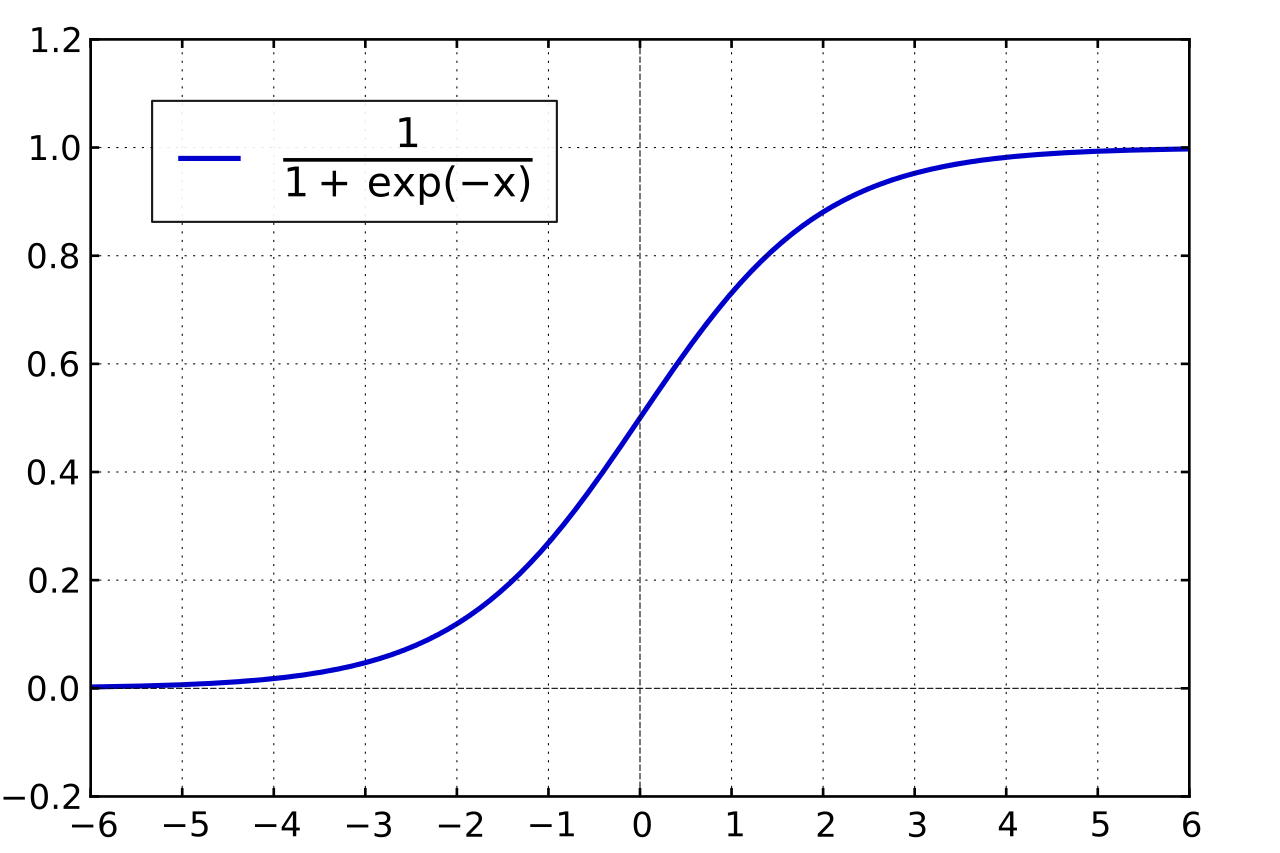
Why use the signmund function for prediction? The s-shaped curve is kind of strange, isn’t it?

Classifications in prediction problems are probabilistic. The model shouldn’t be below zero or higher than one, the s-shaped curve helps to create that. Because of the limits, it can be used for binary classification.

Sigmund function in logistic regression

The function can be used to make predictions.

p(X) = e^(b0 + b1*X) / (1 + e^(b0 + b1*X))

The variable b0 is the bias and b1 is the coefficient for the single input value (x)
This can be rewritten as

ln(odds) = b0 + b1 * X

or

odds = e^(b0 + b1 * X)

To make predictions, you need b0 and b1.

These values are found with the training data.
Initially we set them to zero:

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

Tensorflow will take care of that.

Then the model (based on formula) is:

pred = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax

Where’s the exponent?

The softmax function does the equivalent of:

softmax = tf.exp(logits) / tf.reduce_sum(tf.exp(logits), axis)

Logistic regression with handwriting recognition

Lets use logistic regression for handwriting recognition. The MNIST datset contains 28x28 images of handwritten numbers. Each of those is flattened to be a 784 size 1-d vector.

The problem is:

  • X: image of a handwritten digit
  • Y: the digit value
  • Recognize the digit in the image

The model:

  • logits = X * w + b
  • Y_predicted = softmax(logits)
  • loss = cross_entropy(Y, Y_predicted)

The same in code:

pred = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))

Loss is sometimes called cost.

The code below runs the logistic regression model on the handwriting set. Surprisingly the accuracy is 91.43% for this model. Simply copy and run!


from __future__ import print_function

import tensorflow as tf

# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

# Parameters
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1

# tf Graph Input
x = tf.placeholder(tf.float32, [None, 784]) # mnist data image of shape 28*28=784
y = tf.placeholder(tf.float32, [None, 10]) # 0-9 digits recognition => 10 classes

# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

# Construct model
pred = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax

# Minimize error using cross entropy
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))
# Gradient Descent
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()

# Start training
with tf.Session() as sess:

    # Run the initializer
    sess.run(init)

    # Training cycle
    for epoch in range(training_epochs):
        avg_cost = 0.
        total_batch = int(mnist.train.num_examples/batch_size)
        # Loop over all batches
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            # Run optimization op (backprop) and cost op (to get loss value)
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs,
                                                          y: batch_ys})
            # Compute average loss
            avg_cost += c / total_batch
        # Display logs per epoch step
        if (epoch+1) % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))

    print("Optimization Finished!")

    # Test model
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # Calculate accuracy
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))