Find k for kmeans using the elbow method?

The KMeans algorithm can cluster observed data. But how many clusters (k) are there?

The elbow method finds the optimal value for k (#clusters).

Related course: Complete Machine Learning Course with Python

Determine optimal k

The technique to determine K, the number of clusters, is called the elbow method.

kmeans clustering algorithm

With a bit of fantasy, you can see an elbow in the chart below.

We’ll plot:

  • values for K on the horizontal axis
  • the distortion on the Y axis (the values calculated with the cost function).
    This results in:
    elbow method, determine k, kmeans

When K increases, the centroids are closer to the clusters centroids.

The improvements will decline, at some point rapidly, creating the elbow shape.

That point is the optimal value for K. In the image above, K=3.

Elbow method example

The example code below creates finds the optimal value for k.

 # clustering dataset
# determine k using elbow method

from sklearn.cluster import KMeans
from sklearn import metrics
from scipy.spatial.distance import cdist
import numpy as np
import matplotlib.pyplot as plt

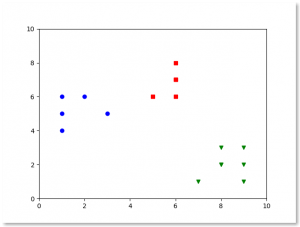
x1 = np.array([3, 1, 1, 2, 1, 6, 6, 6, 5, 6, 7, 8, 9, 8, 9, 9, 8])
x2 = np.array([5, 4, 5, 6, 5, 8, 6, 7, 6, 7, 1, 2, 1, 2, 3, 2, 3])

plt.plot()
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Dataset')
plt.scatter(x1, x2)
plt.show()

# create new plot and data
plt.plot()
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
colors = ['b', 'g', 'r']
markers = ['o', 'v', 's']

# k means determine k
distortions = []
K = range(1,10)
for k in K:
    kmeanModel = KMeans(n_clusters=k).fit(X)
    kmeanModel.fit(X)
    distortions.append(sum(np.min(cdist(X, kmeanModel.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0])

# Plot the elbow
plt.plot(K, distortions, 'bx-')
plt.xlabel('k')
plt.ylabel('Distortion')
plt.title('The Elbow Method showing the optimal k')
plt.show()

If you are new to Machine Learning, I highly recommend this book

Download Machine Learning examples